关于算法的一些基础总结。
算法思想
思想很重要,如果看到需求,能够知道什么思想能够解决这个问题,一般问题的解决就是那么几种思想,需要重点把每种思想都掌握,其实解决题目到最后就是看很清晰的看这个需要要用什么结构体,使用什么样的算法来解决这个问题,解决就是这个思路。工作中也是如此。
其实只有遍历和递归两种基本解决方法,一般都是人使用迭代,神使用递归,所以递归和迭代是解决问题的方法的基本单元,基本都是通过这两种方式解决的,本身确实是思想,但是是方法的思想,和解决问题的算法的思想。所有的问题都是通过迭代或者递归来解决的,但是可以有不同的算法思想,就像数据结构都是数组和链表表示的,但是还是有很多的其他数据结构。
这边简单提一下面试,面试的时候一般就是线性表的考察,树和图在写代码的时候就比较难了,所以要注重线性表的问题,要能把中等以上的题目都写出来,至于树和图只要知道概念和性质用途就行,而且在算法题中中等是门槛,必须写出来,难的有思想解决解析,复杂的数据结构也是这个思路,所以主要线性表的中等和简单问题的思路,要能完全写出来,也符合面试的有效时间内的考察。
基本方法
迭代
迭代就是我们说的遍历,就是我们常规思维,一步步循环走下去,当然有很多技巧或者规律来让我们走的快一点。
递归
递归一般都是生成一颗递归树,一般都是递归回溯的遍历过程。
1.递归过程一般通过函数或子过程实现;
2.递归算法在函数或子过程的内部,直接或间接调用自己的算法
3.递归算法实际上是把问题转化为规模缩小了的同类问题的子问题,然后再递归调用函数或过程来表示问题的解
注意:必须有一个明确的递归结束条件;如果递归次数过多,容易造成栈溢出。
理解递归:递归调用过程中,不要直接一层层走下去,先把简单的第一层走完,哪怕是整个函数,你就当这个为一个表达式,先放在那,你就能很清晰的看到走到哪了
经典运用
阶乘问题
就是典型的一层层的相乘,最后就是N*N-1。。。*1
import "fmt" func factorial(i int)int { if(i <= 1) { return 1 } return i * factorial(i - 1) } func main() { var i int = 15 fmt.Printf("Factorial of %d is %d", i, factorial(i)) }生成括号
递归往数组中加括号,需要生成左括号才能生成右括号,所以需要对括号进行计数left
func generateParenthesis(n int) []string { Output := new([]string) _generate(0, 0, n, "", Output) return *Output } func _generate(left int, right int, max int, s string, Output *[]string){ // 递归终止条件 if left == right && left == max{ *Output = append(*Output, s) return } // 递归主体 if left < max{ _generate(left+1, right, max, s + "(", Output) } if right < left{ _generate(left, right+1, max, s + ")", Output) } }24点
你有 4 张写有 1 到 9 数字的牌。你需要判断是否能通过 *,/,+,-,(,) 的运算得到 24。
直接使用递归遍历,先任意取两个数字,获取其对应四种算法的结果,将其放入到新的数组中,然后再任意获取两个,依次类推,判断最后一位数的时候是否为24就可以。
const ( TARGET = 24 EPSILON = 1e-6 ADD, MULTIPLY, SUBTRACT, DIVIDE = 0, 1, 2, 3 ) func judgePoint24(nums []int) bool { list := []float64{} for _, num := range nums { list = append(list, float64(num)) } return solve(list) } func solve(list []float64) bool { if len(list) == 0 { return false } if len(list) == 1 { return abs(list[0] - TARGET) < EPSILON } size := len(list) for i := 0; i < size; i++ { for j := 0; j < size; j++ { if i != j { list2 := []float64{} for k := 0; k < size; k++ { if k != i && k != j { list2 = append(list2, list[k]) } } for k := 0; k < 4; k++ { if k < 2 && i < j { continue } switch k { case ADD: list2 = append(list2, list[i] + list[j]) case MULTIPLY: list2 = append(list2, list[i] * list[j]) case SUBTRACT: list2 = append(list2, list[i] - list[j]) case DIVIDE: if abs(list[j]) < EPSILON { continue } else { list2 = append(list2, list[i] / list[j]) } } if solve(list2) { return true } list2 = list2[:len(list2) - 1] } } } } return false } func abs(x float64) float64 { if x < 0 { return -x } return x }排列组合
// 最终结果 var result [][]int // 回溯核心 // nums: 原始列表 // pathNums: 路径上的数字 // used: 是否访问过 func backtrack(nums, pathNums []int, used[]bool) { // 结束条件:走完了,也就是路径上的数字总数等于原始列表总数 if len(nums) == len(pathNums) { tmp := make([]int, len(nums)) // 切片底层公用数据,所以要copy copy(tmp, pathNums) // 把本次结果追加到最终结果上 result = append(result, tmp) return } // 开始遍历原始数组的每个数字 for i:=0; i<len(nums); i++ { // 检查是否访问过 if !used[i] { // 没有访问过就选择它,然后标记成已访问过的 used[i] = true // 做选择:将这个数字加入到路径的尾部,这里用数组模拟链表 pathNums = append(pathNums, nums[i]) backtrack(nums,pathNums,used) // 撤销刚才的选择,也就是恢复操作 pathNums = pathNums[:len(pathNums) -1] // 标记成未使用 used[i] = false } } } func permute(nums []int) [][]int { var pathNums []int var used = make([]bool, len(nums)) // 清空全局数组(leetcode多次执行全局变量不会消失) result = [][]int{} backtrack(nums, pathNums, used) return result }应用
组合总和(可重复)
func combinationSum(candidates []int, target int) [][]int { sort.Ints(candidates) res := [][]int{} dfs(candidates, nil, target, 0, &res)//深度优先 return res } func dfs(candidates,nums []int,target,left int,res *[][]int){ if target == 0 { tmp := make([]int,len(nums)) copy(tmp,nums) *res = append(*res,tmp) return } for i:=left;i<len(candidates);i++{ if target < candidates[i] { return } dfs(candidates,append(nums,candidates[i]),target-candidates[i],i,res) } }组合总和(不可重复)
func combinationSum2(candidates []int, target int) [][]int { sort.Ints(candidates) //快排,懒得写 res := [][]int{} dfs(candidates, nil, target, 0, &res) //深度优先 return res } func dfs(candidates, nums []int, target, left int, res *[][]int) { if target == 0 { //结算 tmp := make([]int, len(nums)) copy(tmp, nums) *res = append(*res, tmp) return } for i := left; i < len(candidates); i++ { // left限定,形成分支 if i != left && candidates[i] == candidates[i-1] { // *同层节点 数值相同,剪枝 continue } if target < candidates[i] { //剪枝 return } dfs(candidates, append(nums, candidates[i]), target-candidates[i], i+1, res) //*分支 i+1避免重复 } }第二种方法
func combinationSum3(k int, n int) (ans [][]int) { var temp []int var dfs func(cur, rest int) dfs = func(cur, rest int) { // 找到一个答案 if len(temp) == k && rest == 0 { ans = append(ans, append([]int(nil), temp...)) return } // 剪枝:跳过的数字过多,后面已经无法选到 k 个数字 if len(temp)+10-cur < k || rest < 0 { return } // 跳过当前数字 dfs(cur+1, rest) // 选当前数字 temp = append(temp, cur) dfs(cur+1, rest-cur) temp = temp[:len(temp)-1] } dfs(1, n) return }
思想
枚举算法思想(暴力算法)
将问题的所有可能答案一一列举,根据判断条件判断此答案是否合适,一般用循环遍历迭代实现,就是我们的常规思维。
和回溯的区别就是回溯还有其他的可能,而穷举就是一条路走到黑。但是回溯其实也是暴力破解法,也是一种穷举的算法,回溯一般就是递归实现。
经典运用
求平方根
x的平方根一定在0~x/2之间,然后进行遍历平方对比,可以求近似值a^2<x<(a+1)^2,更加像是数学,比如还有一个牛顿的公式y = ( y + x / y ) / 2 )
func mySqrt(x int) int { if x <= 0 { return 0 } if x<=2{ return 1 } i:=1 for i<=x/2{ if i * i == x { return i } else if i * i > x { if (i-1) * (i-1) < x { return i-1 } }else if i * i < x { i++ } } return i-1 }还有一种取巧的方法,那就是平方根不是n/2,就是n/2+1
func mySqrt(x int) int { if x == 0 { return 0 } ans := int(math.Exp(0.5 * math.Log(float64(x)))) if (ans + 1) * (ans + 1) <= x { return ans + 1 } return ans }查找一个字符串中最长的无重复字串
滑动窗口,重第一个字符串开始遍历,看新的字符在不在遍历的字符串中,如果在,则将左边的位置移动到这个重复字符在遍历字符串中的最后位置的下一个,记录最长的长度进行对比
func lengthOfLongestSubstring(s string) int { if len(s) == 1 { return 1 } var j = 0 var maxLength = 0 for i:=1;i<len(s);i++{ index := strings.Index(s[j:i],string(s[i])) if index == -1 { if i-j +1 > maxLength{ maxLength = i-j +1 } }else{ j = j+index+1 if i-j +1 > maxLength{ maxLength = i-j +1 } } } return maxLength }
贪心算法思想
贪心算法的原理比较简单,就是对问题求解的时候,每步都选择当前的最优解,然后已期望得到全局最优解。用局部最优解叠加出全局最优解。
贪心算法的适用场景是每次选择是没有状态的,也就是不会对后面的步骤产生影响。
局限:
不能保证最后的解是最优的;只能求满足某些约束条件的可行解范围。
经典应用
跳跃游戏
重第一个点开始跳到最远的地方,每一步都是如此以期望达到终点,如果不行,则回退减少一步重试回溯
func canJump(nums []int) bool { goal := len(nums) if goal <= 1 { return true } num := nums[0] for i:=num;i>0;i--{ if i >= goal { return true } if canJump(nums[i:]) { return true } } return false }跳跃游戏2
重第一步开始走,每一步都选择其中最大的一个值,这样可以走的更加远,算法实现居然可以使用迭代,神奇
func jump(nums []int) int { length := len(nums) if length <= 1 { return 0 } index := nums[0] maxIndex := 0 max := 0 times := 0 if index > length { times++ return times }else{ for j:=0;j<index;j++{ if nums[j] > max { max = nums[j] maxIndex = j } } times := jump(nums[maxIndex:]) times++ return times } }分配饼干(最小的饼干不能满足最小的孩子,也不能满足大孩子,如果能满足孩子,后面还有更大的饼干,肯定满足这个孩子,留给后面的)
假设在某次选择中,贪心策略选择给当前满足度最小的孩子分配第 m 个饼干,第 m 个饼干为可以满足该孩子的最小饼干。假设存在一种最优策略,可以给该孩子分配第 n 个饼干,并且 m < n。我们可以发现,经过这一轮分配,贪心策略分配后剩下的饼干一定有一个比最优策略来得大。因此在后续的分配中,贪心策略一定能满足更多的孩子。也就是说不存在比贪心策略更优的策略,即贪心策略就是最优策略。
func findContentChildren(g []int, s []int) int { sort.Ints(g) sort.Ints(s) i,j := 0,0 target := 0 for i < len(g) && j < len(s) { if g[i] <= s[j] { target++ i++ } j++ } return target }不重叠的区间个数
按起点排序,遍历区间,如果不相交则继续移动,如果相交,则取结尾较小的那个,这样留给后面的那个空间选择就较大(贪心),改变其结尾值
func eraseOverlapIntervals(intervals [][]int) int { if len(intervals) == 0 { return 0 } sort.Slice(intervals,func(i,j int)bool{ if intervals[i][0] == intervals[j][0] { return intervals[i][1] < intervals[j][1] } return intervals[i][0] < intervals[j][0] }) end := intervals[0][1] count := 0 for i:=1;i<len(intervals);i++{ if intervals[i][0] >= end { end = intervals[i][1] continue }else{ if intervals[i][1] < end { end = intervals[i][1] } } count++ } return count }摇摆数列,摆动序列
贪心:我们只获取下一个摇摆的项进行状态操作,这样它就是一个摇摆数列,在差值一直为正(负)时,直接过滤,我们值保留最后一个,这样下一个一定是摇摆,可以将正负用状态来表示,进行switch来判断,(状态机),最后在摇摆的时候进行最大长度的增加
func wiggleMaxLength(nums []int) int { if len(nums) < 2 { return len(nums) } begin,up,down := 0,1,2 state := begin maxLen := 1 for i:=1;i<len(nums);i++{ switch state{ case begin: if nums[i] > nums[i-1] { state = down maxLen++ }else if nums[i] == nums[i-1]{ continue }else { state = up maxLen++ } case up: if nums[i] > nums[i-1]{ state = down maxLen++ } case down: if nums[i] < nums[i-1] { state = up maxLen++ } } } return maxLen }移除k个数字(使用如果后一个数字比现在数字小,则删除这个数字的贪心思想)
贪心规律:从高位向低位遍历,如果对应的数字大于下一位数字,则把该位数字去掉,得到的数字最小。去掉 K 个数字,需要从最高位遍历 k 次
注意
1、当所有数字都扫描完成后, k 仍然大于 0,该如何处理? 如: num=12345, k=3:从尾部删除剩余 k 个数字
2、当数字中有 0 出现,该如何特殊处理?如: num=100200, k = 1:如果保留的数字串非空,则保留,否则不保留(比如 00200 无意义)。详情见代码注释
3、如何将最后结果存储为字符串并返回?:Go 中,可以使用 string(‘0’ + number) 的方式转化为字符
func removeKdigits(num string, k int) string { var stack []uint8 // 使用 slice 作为栈 var result string // 存储最终结果字符串 for i := 0; i < len(num); i++ { // 从最高位扫描数字字符串num number := num[i] - '0' // 将字符串转化为整数 // 条件:当栈不为空,且栈顶元素大于下一个数字,且 k 还大于0 for len(stack) != 0 && stack[len(stack)-1] > number && k > 0 { stack = stack[:len(stack)-1] // 弹出栈顶元素 k-- // 剔除一个数字,k 减一 } // 条件:如果数字不为空,或者数字为空但是栈不为空 if number != 0 || len(stack) != 0 { stack = append(stack, number) // 入栈 } } // 条件:如果栈不空且还能删除数字 for len(stack) != 0 && k > 0 { stack = stack[:len(stack)-1] k-- } // 将栈中元素转化为字符串 for _, v := range stack { result += string('0' + v) } // 注意为空情况 if result == "" { return "0" } return result }射击气球
区间排序,重第一个开始遍历选择击穿的区间,一直到第一个不能射中,这个第一个不能射中,需要获取区间的最小的end,再开启第二把射击,依次类推,贪心一次可以击穿最多
func findMinArrowShots(points [][]int) int { if len(points) == 0{ return 0 } sort.Slice(points,func(i,j int) bool { return points[i][0] <= points[j][0] }) count := 1 end := points[0][1] for i:=1;i < len(points);i++{ if end < points[i][0] { end = points[i][1] count++ }else if points[i][1] < end{ end = points[i][1] } } return count }最佳加油方法
在每个加油站都选择最大的加油量,然后在车油能行驶的历程中选择能加到油最多的加油站,这样加油最少次数,这个主要需要注意最后一个加油的情况,和一些加不到油的情况,最好还是要用最大堆来实现
func minRefuelStops(target int, startFuel int, stations [][]int) int { fuel := startFuel if fuel >= target { return 0 } ret := 0 total := &IntHeap{} // 把所以没有加的油存到堆中 heap.Init(total) for i := 0; i < len(stations); i++ { for fuel < stations[i][0] { // 如果目前走不到这个加油站,我们需要加油 if total.Len() == 0 { // 没有油可以加,返回 return -1 } fuel += heap.Pop(total).(int) // 取出最大的油,使用 ret++ } heap.Push(total, stations[i][1]) // 把当前加油站的油放到总池子中,以供下次不够时使用 } for fuel < target { // 如果没有加油站,且不能到达重点,我们需要检查一下是否还有油可以加,直到没有油或者可以到达终点 if total.Len() == 0 { return -1 } fuel += heap.Pop(total).(int) ret++ } return ret } type IntHeap []int func (h IntHeap) Len() int { return len(h) } func (h IntHeap) Less(i, j int) bool { return h[i] > h[j] } func (h IntHeap) Swap(i, j int) { h[i], h[j] = h[j], h[i] } func (h *IntHeap) Push(x interface{}) { *h = append(*h, x.(int)) } func (h *IntHeap) Pop() interface{} { old := *h n := len(old) x := old[n-1] *h = old[0 : n-1] return x }根据身高和序号重组队列
个子矮的人相对于个子高的人是 “看不见” 的,所以可以先安排个子高的人。先排序,然后进行调整,统计前面的高的数量如何和第二位一样了,就讲这个数据插入到目前的位置
func reconstructQueue(people [][]int) [][]int { sort.Slice(people,func(i,j int)bool{ if people[i][0] == people[j][0] { return people[i][1] < people[j][1] } return people[i][0] > people[j][0] }) // 由h、k微调顺序 for i := 1; i < len(people); i++ { // 如果一开始是按照身高降序排序的,这里微调需要从后往前调整 p := people[i] k := p[1] countK := 0 // 统计前边比p高的人数 j := 0 // 如果countK 大于 k,需要把这个娃往前移动,j记录需要移动到的位置 // 如果countK 等于 k,则无需移动;因一开始排序的原因,不会出现countK 小于 k的情况 for ; j < i; j++ { if people[j][0] >= p[0] { countK++ if countK > k { break } } } if countK > k { tmp := []int{p[0], p[1]} _ = copy(people[j+1:i+1], people[j:i]) people[j] = tmp } } return people }
试探算法(回溯法)
在试探算法中,放弃当前候选解,并继续寻找下一个候选解的过程称为回溯。一般都是递归后就是回溯,就是对当前这个值做还是不做处理的两种情况,所以一般用递归实现。 (为求得问题的正确解,会先委婉地试探某一种可能情况。在进行试探过程中,一旦发现原来选择的假设情况是不正确的,马上会自觉地退回一步重新选择,然后继续向前试探。反复进行,直到得到解或证明无解时才死心)
经典运用:
跳跃游戏
尝试所有的可能,如果不行就回溯到开始重新来
八皇后问题(递归回溯遍历)
皇后肯定是一行放一个,每一行放置就是递归,回溯就是确定位置对不对 在每一个递归中都是判断这个位置是否能放,所以要构造一个二维数组bool类型来判断 然后放置一个q,就将他们所有的不能放置的位置置为false 如果下一层不成功说明这个位置不能放置q,也置为false, 依次递归,将数据append到一个数组中去,获取所有的结果。具体看这里。
求子集
递归加入子集,是否取某个数字,这个是否取哪个,取决于是否把数据放到数组中去,递归的就是是否将数据放到数组中去,还可以用栈。
func subsets(nums []int) [][]int { var res [][]int var item []int res = append(res,item) generate(0,item,nums,&res) return res } func generate(i int,item []int, nums []int,res *[][]int){ if i >= len(nums) { return } //选择nums[i] item = append(item,nums[i]) tmp := make([]int,len(item)) copy(tmp,item) *res = append(*res,tmp) generate(i+1,item,nums,res) //不选择nums[i] item = item[:len(item)-1] generate(i+1,item,nums,res) }求子集2
先排序,递归加入子集,是否取某个数字,这个是否取哪个,取决于是否把数据放到数组中去,递归的就是是否将数据放到数组中去,然后在回溯的时候,在放置后的数据的时候需要把和当前元素重复的跳过,这样就不会先相同层级(个数)的相同数据重复选择)可以让同一层级,不出现相同的元素。但是却允许了不同层级之间的重复。
func subsetsWithDup(nums []int) [][]int { sort.Slice(nums,func(i,j int)bool{ return nums[i] < nums[j] }) var item []int var res [][]int generate(0,item,nums,&res) return res } func generate(i int,item []int,nums []int,res *[][]int ){ if i == len(nums) { *res = append(*res,item) return } item = append(item,nums[i]) generate(i+1,item,nums,res) for i+1<len(nums) && nums[i] == nums[i+1] { i++ } item = item[:len(item)-1] generate(i+1,item,nums,res) }其实就是排列组合,扩展应用就是下面的组合数之和。
组合数之和2
采用上面的方法,对每个数组进行求和对比,但是当数值大于target就不参加递归了(剪枝)
func combinationSum2(candidates []int, target int) [][]int { sort.Ints(candidates) //快排,懒得写 res := [][]int{} dfs(candidates, nil, target, 0, &res) //深度优先 return res } func dfs(candidates, nums []int, target, left int, res *[][]int) { if target == 0 { //结算 tmp := make([]int, len(nums)) copy(tmp, nums) *res = append(*res, tmp) return } for i := left; i < len(candidates); i++ { // left限定,形成分支 if i != left && candidates[i] == candidates[i-1] { // *同层节点 数值相同,剪枝 continue } if target < candidates[i] { //剪枝 return } dfs(candidates, append(nums, candidates[i]), target-candidates[i], i+1, res) //*分支 i+1避免重复 } }还可以这样写,其实回溯的过程就是递归深入后回退的过程。
func combinationSum3(k int, n int) (ans [][]int) { var temp []int var dfs func(cur, rest int) dfs = func(cur, rest int) { // 找到一个答案 if len(temp) == k && rest == 0 { ans = append(ans, append([]int(nil), temp...)) return } // 剪枝:跳过的数字过多,后面已经无法选到 k 个数字 if len(temp)+10-cur < k || rest < 0 { return } // 跳过当前数字 dfs(cur+1, rest) // 选当前数字 temp = append(temp, cur) dfs(cur+1, rest-cur) temp = temp[:len(temp)-1] } dfs(1, n) return }
动态规划法
动态规划的核心思想是把原问题分解成子问题进行求解,只要求出子问题的解,就能推断出大问题的解。
比如钞票面额分别是1、5、11,那么我们在凑出15的时候,贪心策略会出错:
15=1×11+4×1 (贪心策略使用了5张钞票)
15=3×5 (正确的策略,只用3张钞票)
为什么会这样呢?贪心策略错在了哪里?因为贪心是一种只考虑眼前情况的策略。
重新分析:我们用f(n)来表示“凑出n所需的最少钞票数量”
取11, cost=f(4)+1
取5, cost=f(10)+1
取1, cost=f(14)+1
这个时候我们要是知道f(4),f(11),f(14)就可以求出需要的张数,我们先不必关心他们是多少,然后在三种方案中只要选择最小的一个数就是我们要的结果,所以
f(n)=min{f(n-1),f(n-5),f(n-11)}+1
这个式子是非常激动人心的。我们要求出f(n),只需要求出几个更小的f值;既然如此,我们从小到大把所有的f(i)求出来不就好了?注意一下边界情况即可。
我们能这样干,取决于问题的性质:求出f(n),只需要知道几个更小的f(n-x)。我们将求解f(n-x)称作求解f(n)的“子问题”,这就是DP(动态规划,dynamic programming).
dp思想是要我们理解把大问题解决为小问题,而实际实现要求我们重一个点开始可以找到所有的从小到大一步步解决所有的问题。
实际应用:
整数拆分
我们可以重0开始,求出每个数字的最大乘积,我们用dp[j]代表j的最大乘积,首先0和1是不可拆分的数字,所以
dp[0]=dp[1]=0 dp[2]=max(1*d[1],1*1) dp[3]=max(max(1*d[2],1*2),max(2*dp[1],2*1)) dp[j]=max(max(1*d[j-1],1*j-1),max(2*dp[j-2],2*j-2)...)在拆分的时候有两种情况,一种是可以继续拆分,一种是不可以继续拆分,这两者大小是要比较的,所以我只要使用动态规划求出所有的最大值,然后对1-j进行遍历对比就,获取最大值
func integerBreak(n int) int { dp := make([]int,n+1) dp[0] = 0 dp[1] = 0 for i:=2;i<=n;i++{ maxi := 0 for j:=1;j<i;j++{ maxj := max(j*dp[i-j],j*(i-j)) maxi = max(maxi,maxj) } dp[i] = maxi } return dp[n] } func max(x,y int)int{ if x>y{ return x } return y }
递推算法思想
1.顺推法:从已知条件出发,逐步推算出要解决问题的方法。
2.逆推法:从已知结果出发,用迭代表达式逐步推算出问题开始的条件,即顺推法的逆过程。
其实就是递归思想。
经典运用:
斐波那契数列(顺推法)
func fib(N int) int { if N == 0 { return 0 } if N == 1 { return 1 } return fib(N-1) + fib(N-2) }
分治算法思想
将一个规模为N的问题分解为K个规模较小的子问题,这些子问题相互独立且与原问题性质相同。只要求出子问题的解,就可得到原问题的解。分治思想一把都是用递归来实现
一般步骤:
1.分解,将要解决的问题划分成若干个规模较小的同类问题
2.求解,当子问题划分得足够小时,用较简单的方法解决
3.合并,按原问题的要求,将子问题的解逐层合并构成原问题的解
经典运用
模拟算法思想
对真实事物或者过程的虚拟。
经典运用
求二进制矩阵中的最短路径
定义方向矩阵,访问矩阵,最短路径矩阵,最短是最先被访问的,然后按方向去遍历,返回最短路径矩阵节点
(1)BFS的问题一般都会选用队列方式实现; (2)代码模板如下: void BFS() { 定义队列; 定义备忘录,用于记录已经访问的位置; 判断边界条件,是否能直接返回结果的。 将起始位置加入到队列中,同时更新备忘录。 while (队列不为空) { 获取当前队列中的元素个数。 for (元素个数) { 取出一个位置节点。 判断是否到达终点位置。 获取它对应的下一个所有的节点。 条件判断,过滤掉不符合条件的位置。 新位置重新加入队列。 } } }代码
func shortestPathBinaryMatrix(grid [][]int) int { dirs := [][]int{{-1, 0}, {-1, 1}, {0, 1}, {1, 1}, {1, 0}, {1, -1}, {0, -1}, {-1, -1}} R := len(grid) C := len(grid[0]) visited := make([][]bool, 0) // 是否遍历过 for range make([]int, R) { // 初始化空的 visited 二维数组 visited = append(visited, make([]bool, C)) } dis := make([][]int, 0) // 到每个顶点的最短路径长度 for range make([]int, R) { dis = append(dis, make([]int, C)) } if grid[0][0] == 1 { // 起始点阻塞 return -1 } if R == 1 && C == 1 { return 1 } //BFS var queue []int // 申请一个队列 queue = append(queue, 0) // 队列添加起始点0 visited[0][0] = true // 起始点已经遍历过了 dis[0][0] = 1 // 起始点记录 for len(queue) > 0 { // 只要队列不为空就继续执行循环 cur := queue[0] // 取出队首元素顶点 queue = queue[1:] // 移除队首元素顶点 curx, cury := cur/C, cur%C // 一维坐标转二维坐标 for d := 0; d < 8; d++ { // 查看顶点周围8个方向的相邻顶点 nextx := curx + dirs[d][0] // 周围8个方向坐标差值 nexty := cury + dirs[d][1] // 相邻顶点坐标(nextx, nexty) // 合法 && 没有被访问过 && 没有被阻塞 if inArea(nextx, nexty, R, C) && !visited[nextx][nexty] && grid[nextx][nexty] == 0 { queue = append(queue, nextx*C+nexty) // 二维坐标转一维坐标入队 visited[nextx][nexty] = true // 记录这个顶点已经被访问过 dis[nextx][nexty] = dis[curx][cury] + 1 // 到该顶点的路径是从cur顶点+1 if nextx == R-1 && nexty == C-1 { // 如果(nextx,nexty)是终点 return dis[nextx][nexty] // 返回到该顶点的距离 } } } } return -1 } func inArea(x, y, R, C int) bool { return x >= 0 && x < R && y >= 0 && y < C }
分支界限法
关键字:解空间(广度优先、最小耗费优先)、界限函数(队列式、优先队列式)
步骤:
1.针对所给问题,定义问题的解空间。问题的解空间应至少包含问题的一个(最优)解
2.确定易于搜索的解空间结构。通常将解空间表示为树、图;解空间树的第i层到第i+1层边上的标号给出了变量的值;从树根到叶子的任一路径表示解空间的一个元素。
3.以广度优先或最小耗费优先的方式搜索整个解空间。每个活节点只有一次机会成为扩展节点,活节点一旦成为扩展节点,其余儿子节点被加入活节点表中。(以此方式递归搜索)
界限函数:分支界限法的核心。尽可能多、尽可能早地“杀掉”不可能产生最优解的活节点。好的界限函数可以大大减少问题的搜索空间,大大提高算法的效率。
1.队列式(FIFO)分支界限法。先进先出
2.优先队列式分支界限法。组织一个优先队列,按优先级选取。通常用最大堆来实现最大优先队列,最小堆来实现最小优先队列。
概率算法
关键词:随机性选择、小概率错误(运行时间大幅减少)、不同解(对同一问题求解两次,可能得到完全不同的解,且所需时间、结果可能会有相当大的差别)
基本特征:
1.输入包括两部分。一,原问题的输入;二,供算法进行随机选择的随机数序列
2.运行过程中,包括一处或多处随机选择,根据随机值来决定算法的运行
3.结果不能保证一定是正确的,但可以限制出错率。
4.不同的运行过程中,对于相同的输入实例可以有不同的结果,执行时间也可能不同。
分类:
1.数值概率算法。常用于数值问题的求解。近似解,近似解的精度随计算时间的增加不断提高。
2.蒙特卡罗(Monte Carlo)算法。精确解,解未必是正确的,正确的概率依赖于算法所用的时间。一般情况下,无法有效地判定所得到的解是否肯定正确。
3.拉斯维加斯(LasVegas)算法。一旦找到解,一定是正确解。找到的概率随计算时间的增加而提高。对实例求解足够多次,使求解失效的概率任意小。
4.舍伍德(Sherwood)算法。总能求得问题的一个解,且所求得的解总是正确的。设法消除最坏情形与特定实例之间的关联性。多用于最快情况下的计算复杂度与其在平均情况下的计算复杂度差别较大。
近似算法
关键词:近似解、解的容错界限(近似最优解与最优解之间相差的程度)、不存在多项式时间算法
基本思想:放弃求最优解,用近似最优解替代最优解。使算法简化,时间复杂度降低
衡量性能的标准:
1.算法的时间复杂度。时间复杂度必须是多项式阶的
2.解的近似程度。与近似算法本身、问题规模、不同的输入实例有关。
示例:NP问题、定点覆盖问题、TSP、子集和数问题、
以上算法思想分的细,有些算法思想其实可以合并一类
时间复杂度和空间复杂度
时间复杂度
我们一般用“大O符号表示法”来表示时间复杂度:T(n) = O(f(n)),n是影响复杂度变化的因子,f(n)是复杂度具体的算法。
时间复杂度就是和算法运行的次数的最高项有关,和运行的次数有关比较好理解,比如运行数得清的几次就能结束的就是O(1),对于n越大运行次数越多的就是O(n),但是和最高项相关的不好理解,比如两个for循环n,其实就是运行的n^2次,这边的2就是最高项,对运行次数有着很大影响的,这边的时间复杂度就是O(n^2)
时间复杂度越简单,说明算法越好:O(1) < O(logn) < O(n) < O(nlogn) < O(n^2) < 。。。
常见的时间复杂度
常数阶O(1)
int a = 1;线性阶O(n)
for(i=1; i<=n; i++) { j = i; j++; }对数阶O(logN)
int i = 1; while(i < n) { i = i * 2; }线性对数阶O(nlogN)
for(m = 1; m < n; m++) { i = 1; while(i < n) { i = i * 2; } }平方阶O(n²)
for(x=1; i <= n; x++){ for(i = 1; i <= n; i++) { j = i; j++; } }立方阶O(n³)
循环三次
K次方阶O(n^k)
循环k次
指数阶(2^n)
空间复杂度
空间复杂度就是和算法占用了多少空间有关系,可以使用空间来换取时间,一般很少有计算这个。
常用
空间复杂度 O(1)
如果算法执行所需要的临时空间不随着某个变量n的大小而变化,即此算法空间复杂度为一个常量,可表示为 O(1)。
空间复杂度 O(n)
int[] m = new int[n] for(i=1; i <= n; ++i) { j = i; j++; }这段代码中,第一行new了一个数组出来,这个数据占用的大小为n,后面虽然有循环,但没有再分配新的空间,因此,这段代码的空间复杂度主要看第一行即可,即 S(n) = O(n)。
经典问题
约瑟夫环
设有编号为1,2,……,n的n(n>0)个人围成一个圈,从第1个人开始报数,报到m时停止报数,报m的人出圈,再从他的下一个人起重新报数,报到m时停止报数,报m的出圈,……,如此下去,直到所有人全部出圈为止。当任意给定n和m后,设计算法求n个人出圈的次序
用循环链表实现:其实就是生成一个环,然后进行数据删除操作,得到序列号
package main
import "fmt"
type LinkNode struct {
Data interface{}
Next *LinkNode
}
type SingleLink struct {
head *LinkNode
tail *LinkNode
size int
}
// 初始化链表
func InitSingleLink()(*SingleLink){
return &SingleLink{
head:nil,
tail:nil,
size:0,
}
}
// 获取头部节点
func (sl *SingleLink)GetHead()*LinkNode{
return sl.head
}
// 获取尾部节点
func (sl *SingleLink)GetTail()*LinkNode{
return sl.tail
}
// 打印链表
func (sl *SingleLink) Print(){
fmt.Println("SingleLink size:",sl.Length())
if sl.size == 0{
return
}
ptr := sl.GetHead()
headNode := sl.GetHead()
for ptr != nil{
fmt.Println("Data:",ptr.Data)
ptr = ptr.Next
if ptr.Next == headNode{
fmt.Println("Data:",ptr.Data)
break
}
}
}
//链表长度
func (sl *SingleLink) Length() int{
return sl.size
}
//插入数据(头插)
func (sl *SingleLink) InsertByHead(node *LinkNode){
if node == nil{
return
}
// 判断是否第一个节点
if sl.Length() == 0{
sl.head = node
sl.tail = node
node.Next = nil
}else{
oldHeadNode := sl.GetHead()
sl.head = node
sl.tail.Next = node
sl.head.Next = oldHeadNode
}
sl.size++
}
//插入数据(尾插)
func (sl *SingleLink) InsertByTail(node *LinkNode) {
if node == nil{
return
}
// 插入第一个节点
if sl.size == 0{
sl.head = node
sl.tail = node
node.Next = nil
}else{
sl.tail.Next = node
node.Next = sl.head
sl.tail = node
}
sl.size ++
}
//插入数据(下标)位置
func (sl *SingleLink) InsertByIndex(index int, node *LinkNode){
if node == nil{
return
}
// 往头部插入
if index == 0 {
sl.InsertByHead(node)
}else{
if index > sl.Length(){
return
}else if index == sl.Length(){
//往尾部添加节点
sl.InsertByTail(node)
}else{
preNode := sl.Search(index-1) // 下标为 index 的上一个节点
currentNode := sl.Search(index) // 下标为 index 的节点
preNode.Next = node
node.Next = currentNode
sl.size++
}
}
}
//删除数据(下标)位置
func (sl *SingleLink) DeleteByIndex(index int) {
if sl.Length() == 0 || index > sl.Length(){
return
}
// 删除第一个节点
if index == 0{
sl.head = sl.head.Next
sl.tail.Next = sl.head
}else{
preNode := sl.Search(index-1)
if index != sl.Length()-1{
nextNode := sl.Search(index).Next
preNode.Next = nextNode
}else{
sl.tail = preNode
preNode.Next = sl.head
}
}
sl.size--
}
// 查询数据
func (sl *SingleLink) Search(index int)(node *LinkNode) {
if sl.Length() == 0 || index > sl.Length(){
return nil
}
// 是否头部节点
if index == 0{
return sl.GetHead()
}
node = sl.head
for i:=0;i<=index;i++{
node = node.Next
}
return
}
func (sl *SingleLink)pop(){
popIndex := 8
delNode := sl.Search(popIndex)
fmt.Println("POP node : ",delNode.Data)
sl.DeleteByIndex(popIndex)
sl.tail = sl.Search(popIndex - 1)
sl.head = sl.Search(popIndex)
fmt.Printf("Head:%v , Tail:%v\n",sl.head.Data,sl.tail.Data)
}
func main() {
// 初始化链表
sl := InitSingleLink()
// 生成30个元素的环
for i:=0;i<30;i++{
snode := &LinkNode{
Data:i,
}
sl.InsertByIndex(i,snode)
}
//循环淘汰第9个元素
var round int
for sl.size > 15{
fmt.Printf("================ Round %d ================\n",round)
sl.pop()
round ++
}
// 获胜者
fmt.Println("================ Finish ================")
fmt.Println("People who survived.")
sl.Print()
}
执行结果
================ Round 0 ================
POP node : 9
Head:10 , Tail:8
================ Round 1 ================
POP node : 19
Head:20 , Tail:18
================ Round 2 ================
POP node : 29
Head:0 , Tail:28
================ Round 3 ================
POP node : 10
Head:11 , Tail:8
================ Round 4 ================
POP node : 21
Head:22 , Tail:20
================ Round 5 ================
POP node : 2
Head:3 , Tail:1
================ Round 6 ================
POP node : 14
Head:15 , Tail:13
================ Round 7 ================
POP node : 26
Head:27 , Tail:25
================ Round 8 ================
POP node : 8
Head:11 , Tail:7
================ Round 9 ================
POP node : 23
Head:24 , Tail:22
================ Round 10 ================
POP node : 6
Head:7 , Tail:5
================ Round 11 ================
POP node : 22
Head:24 , Tail:20
================ Round 12 ================
POP node : 7
Head:11 , Tail:5
================ Round 13 ================
POP node : 25
Head:27 , Tail:24
================ Round 14 ================
POP node : 13
Head:15 , Tail:12
================ Finish ================
People who survived.
SingleLink size: 15
Data: 15
Data: 16
Data: 17
Data: 18
Data: 20
Data: 24
Data: 27
Data: 28
Data: 0
Data: 1
Data: 3
Data: 4
Data: 5
Data: 11
Data: 12
其实这只是一个简单的循环链表的实现,这个环可以用于很多实际场景,比如求第几个人什么时候出列,安排某个人在固定的次序出列,比如下面的魔术师发牌魔术的实现等。
魔术师发牌问题
一位魔术师掏出一叠扑克牌,魔术师取出其中13张黑桃,洗好后,把牌面朝下。 说:“我不看牌,只数一数就能知道每张牌是什么?”魔术师口中念一,将第一张牌翻过来看正好是A; 魔术师将黑桃A放到桌上,继续数手里的余牌, 第二次数1,2,将第一张牌放到这叠牌的下面,将第二张牌翻开,正好是黑桃2,也把它放在桌子上。 第三次数1,2,3,前面二张牌放到这叠牌的下面,取出第三张牌,正好是黑桃3,这样依次将13张牌翻出,全部都准确无误。 求解:魔术师手中牌的原始顺序是什么样子的?
使用数据结构是循环链表:使用13张牌组合成一个循环链表,按1,2。。。遍历对对应的位置进行赋值,跳过已经赋值的位置,就可以实现反向的正确输出。至于JQKA做对应数字的映射就可以了。
package main
import (
"fmt"
"strconv"
)
//13张牌
const len int=13
type Node struct {
order int //牌序号
pNext *Node
}
type playingCard [len]string
//牌用数组存储
func (card *playingCard) newCard(){
card[0]="A"
for i:=1;i<10;i++ {
card[i]=strconv.Itoa(i+1)
}
card[10]="L"
card[11]="Q"
card[12]="K"
}
//建立循环链表
func createList()*Node {
phead:=new(Node)
phead.pNext=nil
q:=phead
for i:=1;i<=len;i++ {
pnew:=new(Node)
pnew.order=-1
q.pNext=pnew
q=pnew
}
q.pNext=phead.pNext
phead=nil
return q
}
//清空链表
func cleanList(list *Node){
p,q:=list.pNext,list.pNext
for p!=list && q!=nil{
q=q.pNext
p=nil
p=q
}
list.pNext=list
}
//销毁链表
func descotry(list *Node){
cleanList(list)
list=nil
}
//发牌
func magic(list *Node) {
count:=1
p:=list.pNext
p.order=0
for count<len {
number:=0
for number<=count{
p=p.pNext
if p.order==-1 {
number++
}
}
p.order=count
count++
}
}
//打印牌
func traverse(list *Node,card playingCard){
p:=list.pNext
for ;p!=list;p=p.pNext {
card.Print(p.order)
//fmt.Printf("%5d",p.order)
}
card.Print(p.order)
//fmt.Printf("%5d",p.order)
}
func (card playingCard) Print(index int) {
if index>=0 && index<len {
fmt.Printf("%5s",card[index])
}else {
fmt.Printf("%5s","空")
}
}
func main() {
var card playingCard
card.newCard()
//fmt.Println(card)
list:=createList()
defer descotry(list)
magic(list)
traverse(list,card)
}
输出结果
$ go run magic.go
A 8 2 5 10 3 Q L 9 4 7 6
汉诺塔
从左到右有A、B、C三根柱子,其中A柱子上面有从小叠到大的n个圆盘,现要求将A柱子上的圆盘移到C柱子上去,期间只有一个原则:一次只能移到一个盘子且大盘子不能在小盘子上面
实现这个算法可以简单分为三个步骤:
- 把n-1个盘子由A 移到 B;
- 把第n个盘子由 A移到 C;
- 把n-1个盘子由B 移到 C;
递归的典型思想,形象的展示了递归回溯的过程
package main
import (
"fmt"
)
func hannuota(n int,A,B,C string){
if n<1 || n>20 {
return
}
if n==1{
fmt.Printf("盘子%d从%s柱子移动到%s柱子\n",n,A,C)
}else {
hannuota(n-1,A,C,B)
fmt.Printf("盘子%d从%s柱子移动到%s柱子\n",n,A,C)
hannuota(n-1,B,A,C)
}
}
func main() {
a,b,c:="A","B","C"
var val int
fmt.Println("请输入要移动的盘子数(1-20之间):N=")
fmt.Scanf("%d",&val)
hannuota(val,a,b,c)
}
运行过程
请输入要移动的盘子数(1-20之间):N=
4
盘子1从A柱子移动到B柱子
盘子2从A柱子移动到C柱子
盘子1从B柱子移动到C柱子
盘子3从A柱子移动到B柱子
盘子1从C柱子移动到A柱子
盘子2从C柱子移动到B柱子
盘子1从A柱子移动到B柱子
盘子4从A柱子移动到C柱子
盘子1从B柱子移动到C柱子
盘子2从B柱子移动到A柱子
盘子1从C柱子移动到A柱子
盘子3从B柱子移动到C柱子
盘子1从A柱子移动到B柱子
盘子2从A柱子移动到C柱子
盘子1从B柱子移动到C柱子
八皇后
「NN 皇后问题」研究的是如何将 NN 个皇后放置在 N \times NN×N 的棋盘上,并且使皇后彼此之间不能相互攻击。
皇后的走法是:可以横直斜走,格数不限。因此要求皇后彼此之间不能相互攻击,等价于要求任何两个皇后都不能在同一行、同一列以及同一条斜线上。
暴力破解方法:重第一行开始每一格都尝试放置皇后,放置的时候检查对应的横直斜方向上是否有皇后,有就不能放,进行下一个,如果都不成功,就进行回溯,用二维数组来表示,用1来表示皇后。
package main
import (
"fmt"
)
const Num int=8
var count int=1
var quees[Num][Num] int
func print(){
fmt.Printf("第%d种解法:\n",count)
for i:=0;i<Num;i++ {
for j:=0;j<Num;j++ {
if quees[i][j]==1 {
fmt.Printf("%s ","■")
}else {
fmt.Printf("%s ","□")
}
}
fmt.Println()
}
}
func setQueen(row,col int) bool {
if row==0 {
quees[row][col]=1
return true
}
for i:=0;i<Num;i++ {
if quees[row][i]==1 {
return false
}
}
for i:=0;i<Num;i++ {
if quees[i][col]==1 {
return false
}
}
for i,j:=row,col;i<Num && j<Num;i,j=i+1,j+1 {
if quees[i][j]==1 {
return false
}
}
for i,j:=row,col;i>=0 && j>=0;i,j=i-1,j-1 {
if quees[i][j]==1 {
return false
}
}
for i,j:=row,col;i<Num && j>=0;i,j=i+1,j-1 {
if quees[i][j]==1 {
return false
}
}
for i,j:=row,col;i>=0 && j<Num;i,j=i-1,j+1 {
if quees[i][j]==1 {
return false
}
}
quees[row][col]=1
return true
}
func solve(row int) {
if row==Num {
print()
count++
return
}
for i:=0;i<Num;i++ {
if setQueen(row,i) {
solve(row+1)
}
quees[row][i]=0
}
}
func main() {
solve(0)
}
常规算法
排序
排序算法是一种元算法,其实排序一般都是为了查找做准备,直接考的很少,但是思想还是有用的。
十大排序算法:冒泡排序、选择排序、插入排序、希尔排序、归并排序、快速排序、堆排序、计数排序、桶排序、基数排序
O(n^2)
插入排序
假设数据都已经排好,然后我用下一个数据向前面已经排好的队列中遍历插入。
func insertionSort(arr []int) []int {
for i := range arr {
preIndex := i - 1
current := arr[i]
for preIndex >= 0 && arr[preIndex] > current {
arr[preIndex+1] = arr[preIndex]
preIndex -= 1
}
arr[preIndex+1] = current
}
return arr
}
选择排序
找到最小的,和第一个交换位置,然后找到剩下最小的,和第二个交换位置,依次类推。这个应该和冒泡是一样的思想,一个把最大的放在最后,一个把最小的放在最前。
func selectSort(arr [6]int) {
for i := 0; i < len(arr)-1; i++ {
min_index := i
for j := i + 1; j < len(arr); j++ {
if arr[i] > arr[j] {
min_index = j
}
arr[i], arr[min_index] = arr[min_index], arr[i]
}
}
fmt.Println(arr)
}
希尔排序
希尔是对插入排序的一种升级,将大的数组分成小的,来插入排序。
/**
希尔排序:把切片分成n个batch,对每个batch进行插入排序;然后减小batch,再对每个batch进行插入排序;直到bathc等于1
*/
func shellSort(arr []int, batchSize int) {
if batchSize < 1 {
return
}
// k : 每个batch中的元素所在batch的index, 介于[0, batchSize)
for k := 0; k < batchSize; k++ {
// 用到了插入排序
for j := 1; batchSize*j+k < len(arr); j++ { // j: 用来获取每个batch所在的第k个元素,拥有多少个batch
for n := j; n > 0; n-- {
pre := batchSize*(n-1) + k
next := batchSize*n + k
if arr[next] < arr[pre] {
arr[next], arr[pre] = arr[pre], arr[next]
}
}
}
}
shellSort(arr, batchSize/2)
}
冒泡排序
比较相邻的元素。如果第一个比第二个大,就交换它们两个; 对每一对相邻元素作同样的工作,从开始第一对到结尾的最后一对,这样在最后的元素应该会是最大的数; 针对所有的元素重复以上的步骤,除了最后一个; 重复步骤1~3,直到排序完成。
就是把最大的先拉出来,其实有一种递归的思想
func bubbleSort(arr [6]int) {
for i := 0; i < len(arr)-1; i++ {
for j := 0; j < len(arr)-i-1; j++ {
if arr[j] > arr[j+1] {
arr[j], arr[j+1] = arr[j+1], arr[j]
}
}
}
fmt.Println(arr)
}
O(nlogn)
快排
使用的是二分法,先选择第一个数据作为基准,然后遍历数据,大于基准的放到一个新的数组中,小于基准的放到一个数组中,依次类推,实现排序。 快排是在冒泡排序的基础上进行递归分治
func quickSort(arr []int) []int {
length := len(arr)
if length <= 1 {
return arr
}
middle := arr[0]
var left []int
var right []int
for i := 1; i < length; i++ {
if middle < arr[i] {
right = append(right, []int{arr[i]}...)
} else {
left = append(left, []int{arr[i]}...)
}
}
middle_s := []int{middle}
left = quickSort(left)
right = quickSort(right)
result := append(append(left, middle_s...), right...)
return result
}
归并排序
归并排序:O(n*log(n)) 建立在归并操作上的一种有效的排序算法。该算法是采用分治法(Divide and Conquer)的一个非常典型的应用 先分治 -> 再合并
//合并
func Merge(arr []int, l, mid, r int) {
// 分别复制左右子数组
n1, n2 := mid-l+1, r-mid
left, right := make([]int, n1), make([]int, n2)
copy(left, arr[l:mid+1])
copy(right, arr[mid+1:r+1])
i, j := 0, 0
k := l
for ; i < n1 && j < n2; k++ {
if left[i] <= right[j] {
arr[k] = left[i]
i++
} else {
arr[k] = right[j]
j++
}
}
for ; i < n1; i++ {
arr[k] = left[i]
k++
}
for ; j < n2; j++ {
arr[k] = right[j]
k++
}
}
//分治
func MergeSort(arr []int, l, r int) {
if l < r {
mid := (l + r - 1) / 2
MergeSort(arr, l, mid)
MergeSort(arr, mid+1, r)
Merge(arr, l, mid, r)
}
}
堆排序
时间复杂度:O(n*log(n))
概念
- 大顶堆:每个节点的值都大于或等于其子节点的值,在堆排序算法中用于升序排列;顶点是最大值
- 小顶堆:每个节点的值都小于或等于其子节点的值,在堆排序算法中用于降序排列;顶点是最小值
- s[0]不用,实际元素从角标1开始
- 父节点元素大于子节点元素
- 左子节点角标为2*k
- 右子节点角标为2*k+1
- 父节点角标为k/2
构造堆
构建最大堆,最小堆,也就是堆的初始化,首先重倒数第二层进行遍历,它的子节点2k,2k+1如果比根节点大,就进行交换,当然交换后如果子节点由树还是需要进行对比交换,直到满足堆的特性,由底想上,最后最大的就在顶上,然后获取堆顶排在第一个,然后剩下的继续构建最大堆。
func HeapSort(s []int) {
N := len(s) - 1 //s[0]不用,实际元素数量和最后一个元素的角标都为N
for k := N / 2; k >= 1; k-- {
sink(s, k, N)
}
//下沉排序
for N > 1 {
s[1], s[N] = s[N], s[1] //将大的放在数组后面,升序排序
N--
sink(s, 1, N)
}
}
//下沉(由上至下的堆有序化)
func sink(s []int, k, N int) {
for {
i := 2 * k
if i > N { //保证该节点是非叶子节点
break
}
if i < N && s[i+1] > s[i] { //选择较大的子节点
i++
}
if s[k] >= s[i] { //没下沉到底就构造好堆了
break
}
s[k], s[i] = s[i], s[k]
k = i
}
}
O(n)
计数排序
计数排序的核心在于将输入的数据值转化为键存储在额外开辟的数组空间中。作为一种线性时间复杂度的排序,计数排序要求输入的数据必须是有确定范围的整数。
func countingSort(arr []int, maxValue int) []int {
bucketLen := maxValue + 1
bucket := make([]int, bucketLen) // 初始为0的数组
sortedIndex := 0
length := len(arr)
for i := 0; i < length; i++ {
bucket[arr[i]] += 1
}
for j := 0; j < bucketLen; j++ {
for bucket[j] > 0 {
arr[sortedIndex] = j
sortedIndex += 1
bucket[j] -= 1
}
}
return arr
}
桶排序
// 桶排序:O(n),是计数排序的升级版,利用的函数的映射关系,这是一个典型的牺牲空间换取时间的排序
// 借助一个一维数组就可以解决这个问题
// 最大数值作为这个数组的长度,数组的下标key等于这元素的,value就+1也就是标记为1
func buckerSort(s []int) []int {
arr := make([]int, 10)
for _, v := range s {
arr[v] += 1
}
sortList := make([]int, 0, len(s))
for k, v := range arr {
if v > 0 {
for i := 0; i < v; i++ {
sortList = append(sortList, k)
}
}
}
return sortList
}
基数排序
基数排序是一种非比较型整数排序算法,其原理是将整数按位数切割成不同的数字,然后按每个位数分别比较。由于整数也可以表达字符串(比如名字或日期)和特定格式的浮点数,所以基数排序也不是只能使用于整数。
比如这样一个数列排序: 342 58 576 356, 以下描述演示了具体的排序过程(红色字体表示正在排序的数位)
第一次排序(个位):
3 4 2
5 7 6
3 5 6
0 5 8
第二次排序(十位):
3 4 2
3 5 6
0 5 8
5 7 6
第三次排序(百位):
0 5 8
3 4 2
3 5 6
5 7 6
结果: 58 342 356 576
实例
// 基数排序
func BaseSort(data []int) []int {
if len(data) < 2 {
return data
}
max := data[0]
dataLen := len(data)
for i := 1; i < dataLen; i++ {
if data[i] > max {
max = data[i]
}
}
// 计算最大值的位数
maxDigit := 0
for max > 0 {
max = max/10
maxDigit++
}
// 定义每一轮的除数,1,10,100...
divisor := 1;
// 定义了10个桶,为了防止每一位都一样所以将每个桶的长度设为最大,与原数组大小相同
bucket := [10][20]int{{0}}
// 统计每个桶中实际存放的元素个数
count := [10]int{0}
// 获取元素中对应位上的数字,即装入那个桶
var digit int
// 经过maxDigit+1次装通操作,排序完成
for i := 1; i <= maxDigit; i++ {
for j := 0; j < dataLen; j++ {
tmp := data[j]
digit = (tmp / divisor) % 10
bucket[digit][count[digit]] = tmp
count[digit]++
}
// 被排序数组的下标
k := 0
// 从0到9号桶按照顺序取出
for b := 0; b < 10; b++ {
if count[b] == 0 {
continue
}
for c := 0; c < count[b]; c++ {
data[k] = bucket[b][c]
k++
}
count[b] = 0
}
divisor = divisor * 10
}
return data
}
这三种排序算法都利用了桶的概念,但对桶的使用方法上有明显差异:
基数排序:根据键值的每位数字来分配桶;
计数排序:每个桶只存储单一键值;
桶排序:每个桶存储一定范围的数值;
语言应用
查找
分类
静态查找和动态查找;
注:静态或者动态都是针对查找表而言的。动态表指查找表中有删除和插入操作的表。
无序查找和有序查找。
无序查找:被查找数列有序无序均可;
有序查找:被查找数列必须为有序数列。
常见查找方法
七大查找算法:顺序查找、二分查找、差值查找、斐波那契查找、 树表查找 (二叉树查找、平衡查找树之2-3查找树、平衡查找树之红黑树、B树和B+树)、分块查找、哈希查找、图查找 (广度优先查找、深度优先查找)
循序迭代查找
查找结构:线性表(数组和链表),无序
就是我们最常用的迭代遍历,找到了就返回
二分查找
查找结构:有序的,非动态的数组
也是我们常说的折半查找,一般是获取中间数据,进行对比,需要查找的数据在左边一半还是在右边一半,依次类推,进行递归。
func binarySearch(arr []int, k int) int { left, right, mid := 1, len(arr), 0 for { // mid向下取整 mid = int(math.Floor(float64((left + right) / 2))) if arr[mid] > k { // 如果当前元素大于k,那么把right指针移到mid - 1的位置 right = mid - 1 } else if arr[mid] < k { // 如果当前元素小于k,那么把left指针移到mid + 1的位置 left = mid + 1 } else { // 否则就是相等了,退出循环 break } // 判断如果left大于right,那么这个元素是不存在的。返回-1并且退出循环 if left > right { mid = -1 break } } // 输入元素的下标 return mid } func binarySearch2(sortedArray []int, lookingFor int) int { var low int = 0 var high int = len(sortedArray) - 1 for low <= high { var mid int =low + (high - low)/2 var midValue int = sortedArray[mid] if midValue == lookingFor { return mid } else if midValue > lookingFor { high = mid -1 } else { low = mid + 1 } } return -1 } func binarySearch3(arr []int, k int) int { low := 0 high := len(arr) - 1 for low <= high { // 这种写法防止两数和导致的内存溢出 mid := low + (high-low)>>1 // avg=(a+b)>>1://右移表示除2,左移表示乘2 if k < arr[mid] { high = mid - 1 } else if k > arr[mid] { low = mid + 1 } else { return mid } } return -1 } func binarySearch4(arr []int, k int) int { low := 0 high := len(arr) - 1 for low <= high { /** 利用位与(&)提取出两个数相同的部分,利用异或(^)拿出两个数不同的部分的和,相同的部分加上不同部分的和除2即得到两个数的平均值 异或: 相同得零,不同得1 == 男男等零,女女得零,男女得子 avg = (a&b) + (a^b)>>1; 或者 avg = (a&b) + (a^b)/2; */ mid := low & high + (low ^ high) >> 1 if k < arr[mid] { high = mid - 1 } else if k > arr[mid] { low = mid + 1 } else { return mid } } return -1 } 第三、第四种方法逼格最高,第四种效率最快差值查找
查找结构:有序的,非动态的数组
是在二分查找的基础上进行优化,不在取中间值,而是取我们查找的数据的比例,这样查找更快,但是比较适合数据比较均匀的,否则效果很差,其他一样。
func insertSearch(arr []int, key int) int{ low := 0 high := len(arr) - 1 time := 0 for low < high { time += 1 // 计算mid值是插值算法的核心代码 实际上就是 mid := low + int((high - low) * (key - arr[low])/(arr[high] - arr[low])) if key < arr[mid] { high = mid - 1 }else if key > arr[mid] { low = mid + 1 }else { return mid } } return -1 }还可以升级为斐波那契查找,就是将数据分为数量比例为0.618的两份进行查找。
树
树的查找主要在于树的构建,满足了特性,查找就变的简单。
二叉排序树
查找结构:树,必须满足二叉排序树的特点
就是所有的左节点都小于根节点,所有的右节点都大于根节点,这样中序遍历的适合就是一个有序数组。而且查找类似于二分查找。更快。
二叉查找树是先对待查找的数据进行生成树,确保树的左分支的值小于右分支的值,然后再用所查数据和每个节点的父节点比较大小,查找最适合的范围。 这个算法的查找效率很高,但是如果使用这种查找方法要首先创建树。
需要先构造一个二叉树,然后把数组的元素和索引放置树的对应位置,然后在从输的root逐个换个key做对比,取出key所在数组中的index
/** 基本思路:先把数组构造出一颗二叉树的样纸,然后查找的时候在从root往下对比 */ func BSTsearch(arr []int, key int) int{ // 先在内存中构造 二叉树 tree := new(Tree) for i, v := range arr { Insert(tree, v, i) } // 开始二叉树查找目标key return searchKey(tree.Root, key) } // 节点结构 type Node struct { Value, Index int // 元素的值和在数组中的位置 Left, Right *Node } // 树结构 type Tree struct { Root *Node } // 把数组的的元素插入树中 func Insert(tree *Tree, value, index int){ if nil == tree.Root { tree.Root = newNode(value, index) }else { InsertNode(tree.Root, newNode(value, index)) } } // 把新增的节点插入树的对应位置 func InsertNode(root, childNode *Node) { // 否则,先和根的值对比 if childNode.Value <= root.Value { // 如果小于等于跟的值,则插入到左子树 if nil == root.Left { root.Left = childNode }else { InsertNode(root.Left, childNode) } }else{ // 否则,插入到右子树 if nil == root.Right { root.Right = childNode }else { InsertNode(root.Right, childNode) } } } func newNode(value, index int) *Node { return &Node{ Value: value, Index: index, } } // 在构建好的二叉树中,从root开始往下查找对应的key 返回其在数组中的位置 func searchKey(root *Node, key int) int { if nil == root { return -1 } if key == root.Value { return root.Index }else if key < root.Value { // 往左子树查找 return searchKey(root.Left, key) }else { // 往右子树查找 return searchKey(root.Right, key) } }平衡二叉排序树(AVL树)
在二叉排序树的基础上进行平衡,因为二叉排序树在一些极端情况,比如斜树,效率很差,而且这情况是可以转化为效率高的左右平衡的情况, 所以我们定义左右子树的度相差不能超过1的树叫平衡二叉排序树(AVL树),这样的树查找效率就得到来保证,如何平衡,就是在每次树插入时 判断一下度的差距(左-右),如果小于-1则左旋转,大于1则右旋转。
-
红黑树是一种基于二叉查找树的数据结构,是一种自平衡的二叉搜索树,它包含了二叉搜索树的特性,但是为什么还要红黑树呢?因为是一种弱平衡二叉树(由于是若平衡,可以推出,相同的节点情况下,AVL树的高度低于红黑树),相对于要求严格的AVL树来说,它的旋转次数变少,所以对于搜索,插入,删除操作多的情况下,我们就用红黑树.
能用平衡树的地方,就可以用红黑树。用红黑树之后,读取略逊于AVL,维护强于AVL。设计红黑树的目的,就是解决平衡树的维护起来比较麻烦的问题,红黑树,读取略逊于AVL,维护强于AVL,每次插入和删除的平均旋转次数应该是远小于平衡树。
实例
const ( RED = true BLACK = false ) // 节点 type RBNode struct { Color bool // true == 红 false == 黑 Parent, Left, Right *RBNode Value, Index int } type RBTree struct { Root *RBNode } /* * 对红黑树的节点(x)进行左旋转 * * 左旋示意图(对节点 x 进行左旋): * px px * / / * x y * / \ --(左旋)-. / \ # * lx y x ry * / \ / \ * ly ry lx ly * * */ func (t *RBTree) leftSpin(node *RBNode) { // 先提出自己的 右子 y := node.Right // 自己的新右子 是前右子的左子 node.Right = y.Left if nil != y.Left { y.Left.Parent = node } // 你以前的爹,就是我现在的爹 y.Parent = node.Parent // 如果被旋转的节点是 之前树的根 // 那么,新的跟就是 y 节点 if nil == node.Parent { t.Root = y } else { // 被旋转的是普通节点时, 需要结合自身的父亲来确认自己之前是属于 左子还是右子 if node.Parent.Left == node { // 被旋转节点之前是 左子时 // 用 y 来作为之前 该节点父亲的 新左子 node.Parent.Left = y } else { // 否则,是 右子 node.Parent.Right = y } } // 将 node 设为 y 的左子 y.Left = node // 将 y 设为 node 的新父亲 node.Parent = y } /* * 对红黑树的节点(y)进行右旋转 * * 右旋示意图(对节点 y 进行左旋): * py py * / / * y x * / \ --(右旋)-. / \ # * x ry lx y * / \ / \ # * lx rx rx ry * */ func (t *RBTree) rightSpin(node *RBNode) { // 先提出自己的 左子 x := node.Left node.Left = x.Right if nil != x.Left { x.Right.Parent = node } x.Parent = node.Parent // 如果被旋转的节点是 之前树的根 // 那么,新的跟就是 x 节点 if nil == node.Parent { t.Root = x } else { if node.Parent.Right == node { node.Parent.Right = x } else { node.Parent.Left = x } } x.Right = node node.Parent = x } func insertValue(tree *RBTree, val, index int) { node := &RBNode{Value: val, Index: index, Color: BLACK} if nil == tree.Root { tree.Root = node }else{ tree.insert(node) } } func (t *RBTree) insert(node *RBNode) { //int cmp; var tmpNode *RBNode root := t.Root // 1. 将红黑树当作一颗二叉查找树,将节点添加到二叉查找树中。 for nil != root { if node.Value < root.Value { root = root.Left } else { root = root.Right } tmpNode = root } node.Parent = tmpNode if nil != tmpNode { if node.Value < tmpNode.Value { tmpNode.Left = node } else { tmpNode.Right = node } } else { t.Root = node } // 2. 设置节点的颜色为红色 node.Color = RED // 3. 将它重新修正为一颗二叉查找树 t.adjustRBTree(node) } // 修正树 func (t *RBTree) adjustRBTree(node *RBNode) { var parent, gparent *RBNode // 父亲 和 祖父 // 若“父节点存在,并且父节点的颜色是红色” for nil != node.Parent && RED == node.Parent.Color { parent = node.Parent gparent = parent.Parent //若“父节点”是“祖父节点的左孩子” if parent == gparent.Left { // Case 1条件:叔叔节点是红色 uncle := gparent.Right if nil != uncle && RED == uncle.Color { uncle.Color = BLACK parent.Color = BLACK gparent.Color = RED node = gparent continue } // Case 2条件:叔叔是黑色,且当前节点是右孩子 if node == parent.Right { var tmp *RBNode t.leftSpin(parent) tmp = parent parent = node node = tmp } // Case 3条件:叔叔是黑色,且当前节点是左孩子。 parent.Color = BLACK gparent.Color = RED t.rightSpin(gparent) } else { //若“z的父节点”是“z的祖父节点的右孩子” // Case 1条件:叔叔节点是红色 uncle := gparent.Left if nil != uncle && RED == uncle.Color { uncle.Color = BLACK parent.Color = BLACK gparent.Color = RED node = gparent continue } // Case 2条件:叔叔是黑色,且当前节点是左孩子 if node == parent.Left { var tmp *RBNode t.rightSpin(parent) tmp = parent parent = node node = tmp } // Case 3条件:叔叔是黑色,且当前节点是右孩子。 parent.Color = BLACK gparent.Color = RED t.leftSpin(gparent) } } // 将根节点设为黑色 t.Root.Color = BLACK } /** 红黑树查找 */ func RedBlackTreeSearch(arr []int, key int) int{ // 先构造树 tree := new(RBTree) for i, v := range arr { insertValue(tree, v, i) } // 开始二叉树查找目标key return tree.serch(key) } func (t *RBTree) serch(key int) int { return serch(t.Root, key) } func serch(node *RBNode, key int) int { if nil == node { return -1 } if key < node.Value { return serch(node.Left, key) }else if key > node.Value { return serch(node.Right, key) }else { return node.Index } } -
多路树使得树结构更加矮胖,这样更加能够减少查询的次数,增加查询的效率。一般数据库的索引就是使用多路树,维护困难,查找效率高。
B和B+树主要用在文件系统以及数据库做索引.比如Mysql;
- 红黑树多用在内部排序,即全放在内存中的,STL的map和set的内部实现就是红黑树。
- B+树多用于外存上时,B+也被成为一个磁盘友好的数据结构。
-
深度优先查找和广度优先查找,算是比较复杂的查找,一般也是在复杂的场景下使用。
索引查找
- 稠密索引 新建一个索引数组,在每个数据后加一个指针指向数据所在的位置,类似于一个哈希表,只实用于数据比较少的情况。
分块索引 新建一个索引表,存储一块数据的最大值和开始位置,每块数据是要进行排序的,但是块内的数据是不需要排序的,这样查找直接查到到哪一块。
是顺序查找的一种结合改进;
将n个数据元素”按块有序”划分为m块(m ≤ n)。每一块中的结点不必有序,但块与块之间必须”按块有序”;即第1块中任一元素的关键字都必须小于第2块中任一元素的关键字;而第2块中任一元素又都必须小于第3块中的任一元素,…… 算法流程:
step1 :先选取各块中的最大关键字构成一个索引表; step2 :查找分两个部分:先对索引表进行二分查找或顺序查找,以确定待查记录在哪一块中;然后,在已确定的块中用顺序法进行查找。倒排索引 用关键字来指向在哪些文件中存在,也就是我们的反向索引,和我们正常思想相反,正常的正向索引就是每个文件中包含哪些关键字,倒排索引更利于查找。
快慢指针
一个指针走的快,一个走的慢,两个指针之间拥有一定的规律。比如
1、解决查找不知道大小的链表的中间数问题
可以使用两个指针,一个一次走两位,一个指针一次走一位,两者之间就是两倍的关系,当快指针走到最后,慢指针刚好是获取中间2、解决链表是否有环问题
两个指针一个指针一步步移动,另一个指针则直接重头移动到第二个指针的位置,两者所使用的步数不同,就可以确认是有环的。堆查找
topK– 孤岛算法:TOP k就是从海量的数据中选取最大的k个元素或记录。
基本思想:就是维护一个具有k个元素的最小堆【小顶堆】。每当有新的元素加入时,判断它是否大于堆顶元素,如果大于,用该元素代替堆顶元素,并重新维护小顶堆,直到所有元素被处理完毕。
时间复杂度为O(N*logk),基本达到线性复杂度。
适用场景:
无序的,海量数据的代码:
func HeapSearchK (arr []int, topk int) { // 初始化原始最小堆 smallHeapArr := buildSmallHeap(arr, topk) for i := topk; i < len(arr); i ++ { // 如果当前原始比最小堆的根元素大,那么替换根,且重新调整最小堆 if arr[i] > smallHeapArr[0] { swapRoot(smallHeapArr, arr[i]) } } // 最大的K个数 fmt.Println(smallHeapArr) } //建立小顶堆 func buildSmallHeap(arr []int,topk int) []int{ smallHeapArr := arr[:topk] for i := topk>>1 - 1; i >= 0; i-- { adjustSmallHeap(smallHeapArr, i, topk) } return smallHeapArr } // 调整最小堆 func adjustSmallHeap(arr []int, parent, length int) { i := parent for { lchild := 2*parent + 1 rchild := 2 *parent + 2 if lchild < length && arr[lchild] < arr[i] { i = lchild } // 右节点和根 if rchild < length && arr[rchild] < arr[i]{ i = rchild } // 互换位置 if parent != i { arr[i], arr[parent] = arr[parent], arr[i] parent = i }else { break } } } // 替换根部,且重新构造最小堆 func swapRoot(arr []int, root int) { arr[0] = root // 新的根 // 重新调整堆 adjustSmallHeap(arr, 0, len(arr)) }哈希查找
哈希查找的核心在于哈希表的构建,有了哈希表,就可以直接找到key对应的值。
哈希表可以是二维数组,也可以是数组加链表。
说白了就是用一个二维数组来装原数组经过Hash运算后的值,如,第一维是 元素Hash后的值,第二维依次装着该 key在原数组中出现的索引号 <因为原数组中的 元素可能会有相同的,所以Hash值也会一样,所以用了二维数组>。在查找的时候可以先计算Hash然后用顺序查找在第一维中找到对应的Hash,然后在第二维中依次返回里面的内容<也就是该key在原数组中的索引值>;如果没找到对应Hash,则原数组没有包含该key
哈希表是一种数据结构,但是它并没有准确的结构类型,我觉得可以说是一种概念,类似于数组,只不过它的索引是key,是要单独存储的,然后根据key通过hash函数可以直接访问存储结构地址。但是会发送索引相同的情况,这个时候解决这种冲突的方法决定了最终的数据结构。
拉链法
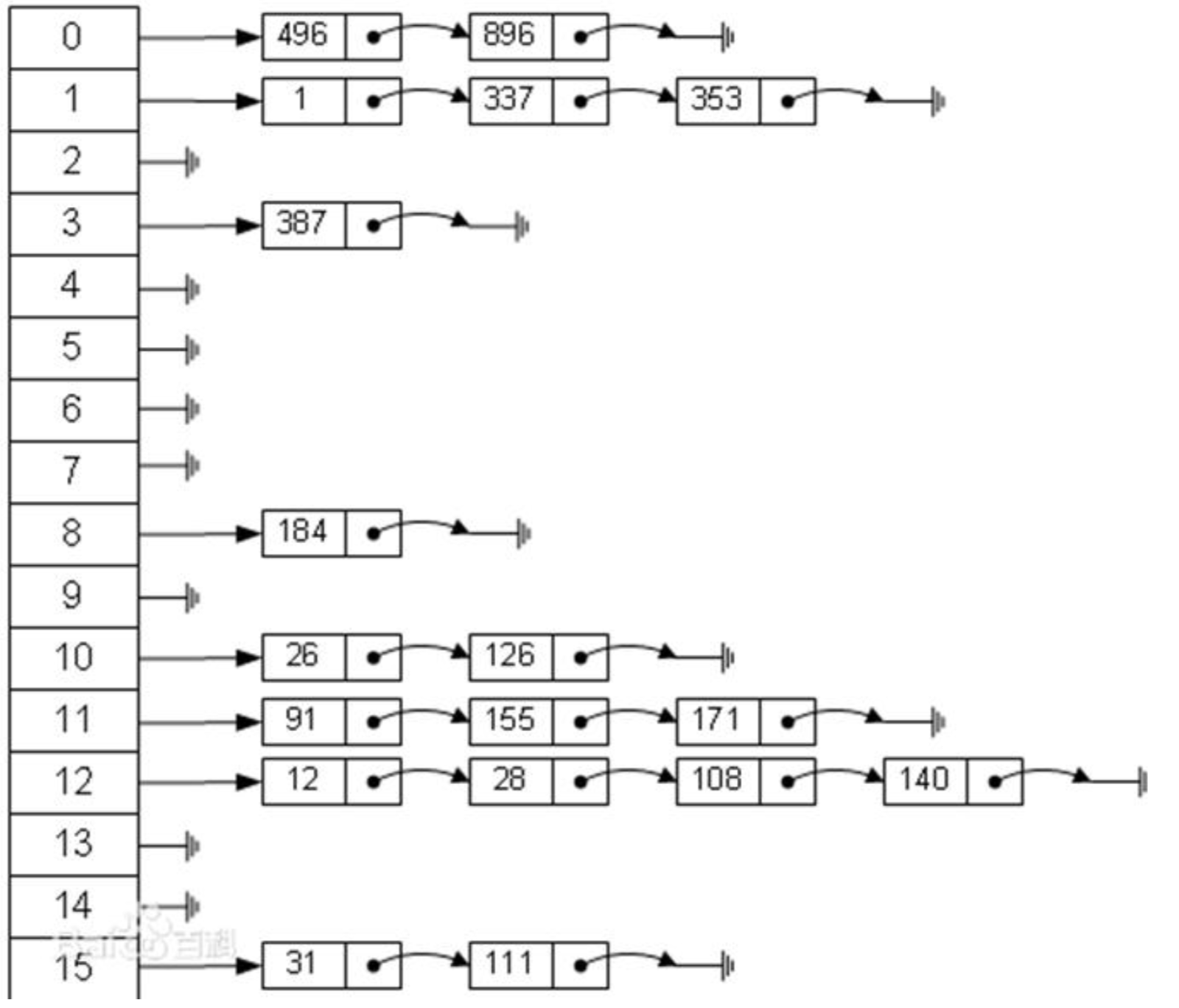
拉链是指将数组指向一个链表,链表有对应的key-value且属于同一索引组成,然后再根据key匹配到对应的值。通过一个哈希函数将key转换为数组下标,真正的key-value是存储在该数组对应的链表里。
这也就是我们常说的hashmap,使用了数组和链表的结合,结构如下
代码结构
//链表结构里数据的数据类型 键值对 type KV struct { Key string Value string } //链表结构 type LinkNode struct { //节点数据 Data KV //下一个节点 NextNode *LinkNode } type HashMap struct { //HashMap木桶 Buckets [BucketCount]*LinkNode }开放寻址法
线性探测:将key-value存放在数组中,发现没有数据,就在这个地址存储,发现有数据,则把同一索引的顺延往下存放。
这个单纯的使用数组进行实现。
代码结构
//链表结构里数据的数据类型 键值对 type KV struct { Key string Value string } type Hasharray struct { Buckets []KV }
哈希函数:time33
数据较少的时候可以用直接定址,用一个线性函数完成映射,空间复杂度高一点 一般用除余法,选择一个较大的素数。一般最好是接近或者等于哈希表的长度。 数字选择法,在key过大的时候。
应用
在一个文件中有 10G 个整数,乱序排列,要求找出中位数。内存限制为 2G。只写出思路即可(内存限制为 2G的意思就是,可以使用2G的空间来运行程序,而不考虑这台机器上的其他软件的占用内存)。
关于中位数:数据排序后,位置在最中间的数值。即将数据分成两部分,一部分大于该数值,一部分小于该数值。中位数的位置:当样本数为奇数时,中位数=(N+1)/2 ; 当样本数为偶数时,中位数为N/2与1+N/2的均值(那么10G个数的中位数,就第5G大的数与第5G+1大的数的均值了)。
其实这题就是在让我们思考如何获取海量数据的中位数,一共有几种思想:
1、外排序
先将这10G的数据等分成5份存储到硬盘中,然后依次读入一份到内存里面,进行排序,然后将这5份数据进行归并得到最后的排序结果,然后找出中位数第5G大
2、堆排序
利用堆排序处理海量数据的topK是非常合适不过了,因为它不用将所有的元素都进行排序,只需要比较和根节点的大小关系就可以了,同时也不需要一次性将所有的数据都加载到内存;对于海量数据而言,要求前k小/大的数,我们只需要构建一个k个大小的堆,然后将读入的数依次和根节点比较就行了。
对于10G的数据,它的中位数就是第5G个元素,按常理来说我们需要构建一个5G大小的堆,但是允许的内存只有两个G,所以我们先构建一个1G大小的大顶堆,然后求出第1G个元素(根节点),然后利用该元素构建一个新的1G大小的堆,求出第2G大的元素,依次类推,求出第5G大的元素
3、分而治之:基于二进制位映射分割
依次读入一部分数据到内存,根据数据的最高位将数据映射到不同的文件中,然后判断中位数可能存在于于哪个文件然后再继续对哪个文件进行分割,知道能够将数据读入内存直接排序
4、计数排序
先知道这个数据属于什么范围,然后每个数据的大小作为数组的下标,对这个统计的次数作为数组的值,遍历一遍过后可以统计出数据的大致分布,求出中间次数就行
5、基数排序
先对最低位进行排序,再依次对高位进行排序,最后对一个顺序数组取中位数。
6、桶排序
桶排序其实就是基数排序的升级,将一段数据映射到一个桶中去,减少桶的使用
假设这10G数据都是32位的无符号整数,那么每个数的值域为(0,2 ^ 32 -1)
(1)我们不可能创建2^32个桶,空间复杂度太大,所以我们创建2 ^16个桶
(2)由于我们的内存只有2G,所以一次读取2G数据,按照某种映射关系映射到对应的桶里面
(3)依次统计每个桶里面的数据,找到中位数的范围,在针对范围中的数据进行排序,找到中位数的具体位置
7、位排序
假设10G数据都为无符号整数(范围为0-2^32),考虑到可能原数据中可能有重复,所以我们采用两个bit位来表示一个整数,00表示为出现,01表示出现1次,10表示出现多次
所需要的内存为1G
对于10G的数据我们只需要1G的内存就能够表示出来所有的数据,可见bitmap的压缩性之强
我们依次读取10G数据,然后转换为位图表示,去掉所有bit位为00的位置,找到中间下标就是中位数
蓄水池抽样算法
蓄水池算法适用于对一个不清楚规模的数据集进行采样。算法实现
- 假设数据序列的规模为 𝑛,需要采样的数量的为 𝑘。
- 首先构建一个可容纳 𝑘 个元素的数组,将序列的前 𝑘 个元素放入数组中。
- 然后从第 𝑘+1 个元素开始,以 𝑘𝑛 的概率来决定该元素是否被替换到数组中(数组中的元素被替换的概率是相同的)。 当遍历完所有元素之后,数组中剩下的元素即为所需采取的样本。
数学证明每个元素被取到的概率都是k/n。
核心算法代码
int[] reservoir = new int[m];
// init
for (int i = 0; i < reservoir.length; i++)
{
reservoir[i] = dataStream[i];
}
for (int i = m; i < dataStream.length; i++)
{
// 随机获得一个[0, i]内的随机整数
int d = rand.nextInt(i + 1);
// 如果随机整数落在[0, m-1]范围内,则替换蓄水池中的元素
if (d < m)
{
reservoir[d] = dataStream[i];
}
}
以前在某个地方看到过一个面试题,说是从一个字符流中进行采样,最后保留 10 个字符,而并不知道这个流什么时候结束,且须保证每个字符被采样到的几率相同。用的就是这个算法。